turtle画奥运五环 给了起点坐标_turtle绘制奥运五环

turtle画奥运五环 给了起点坐标_turtle绘制奥运五环

       好的，现在我来为大家谈一谈turtle画奥运五环 给了起点坐标的问题，希望我的回答能够解答大家的疑惑。关于turtle画奥运五环 给了起点坐标的话题，我们开始说说吧。

1.用CAD2007画直线，输入起点坐标后,为什么起点总是画在默认坐标点上,而不是我指定的坐标点

2.关于CAD审图、绘图，重难点的学习经验有哪些？

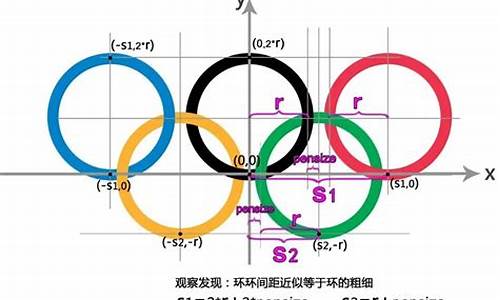
3.Python的turtle库画图使用中的问题

4.如何用python turtle画斐波那契螺旋曲线？

用CAD2007画直线，输入起点坐标后,为什么起点总是画在默认坐标点上,而不是我指定的坐标点

       你是不是在捕捉状态下？如果你的这个坐标点离这个附近的可捕捉的特殊点太近，就会被“吸引”过去，画到捕捉点上去了。解决办法是用F3键临时关闭捕捉状态。还有一种可能：你给出的坐标是二维的，但是你想画到Z值不为零的平面上去，即Z坐标不为零却没有给出，就会落到当前的XOY平面中去了。

关于CAD审图、绘图，重难点的学习经验有哪些？

       首先在Excel中把坐标值做出来：

       A1：X；B1：Y（y=x^2）；C1：A1&“，"&B1。得出的C1就是坐标值；把A列往下托得出A2、A3；把B列往下托得出B2、B3，把C列往下托得出C2、C3。将C列复制。

       打开CAD输入命令"pl"多段线命令，回车，在命令处右击，把刚从Excel中复制的C列数据粘贴到命令行处，这样就可生成抛物线了。

       ezplot('y=x^2')

       x=-1：0.01：1；

       y=x^2；

       plot（x，y）；

       简介

       在数学中，抛物线是一个平面曲线，它是镜像对称的，并且当定向大致为U形（如果不同的方向，它仍然是抛物线）。它适用于几个表面上不同的数学描述中的任何一个，这些描述都可以被证明是完全相同的曲线。

       抛物线的一个描述涉及一个点（焦点）和一条线（准线）。焦点并不在准线上。抛物线是该平面中与准线和焦点等距的点的轨迹。抛物线的另一个描述是作为圆锥截面，由圆锥形表面和平行于锥形母线的平面的交点形成。第三个描述是代数。

Python的turtle库画图使用中的问题

       第一部分：

       01.

       审图：本题主要是用相对坐标画图，各点的坐标都可以计算出来。

       绘图步骤：先建立两个图层，一个绘图，一个作为尺寸标注。绘图时，从原点（0,0）开始画外框，从点（14,8）开始画内框，主要使用Line并且打开正交模式依次画出各个线段即可。接下来按原图进行尺寸标注。

       重点难点：确定内框起点坐标、正交模式。

       02.

       审图：本题使用相对坐标画图，需建立两个图层分别是绘图、尺寸标注图层；利用正交模式画水平线竖直线和利用极坐标追踪模式画斜线。

       03.

       审图：本题使用相对坐标画图，需建立两个图层分别是绘图、尺寸标注图层；计算各点的相对坐标，利用正交模式画出各段线段，内外框分别画出。

       绘图步骤：先建立两个图层分别是绘图、尺寸标注图层；外框从两个方向（上、右）利用正交模式画，内框从点（10,6）开始，利用正交模式和相关线段尺寸画出；最后按照原图进行尺寸标注。

       重点难点：利用正交模式、内框的左下点坐标、尺寸标注的连续标注。

       04.

       审图：本题使用相对坐标画图，需建立两个图层分别是绘图、尺寸标注图层；计算各段线段的长度，水平、竖直线用正交模式画，斜线用极轴追踪模式并且在已知角度和长度的情况下绘出；内外框分别作图。

       绘图步骤：先建立两个图层分别是绘图、尺寸标注图层；外框从点（0,0）开始，分别沿上、右两个方向画各线段，至于斜线段可使用极坐标追踪模式在已知角度和长度的情况下画出；内框从点（11,10）开始，上端线先画一条水平长点的直线，画相应斜线与其相交，再修剪即可；最后进行尺寸标注。

       重点难点：各段线段的计算、斜直线的绘画（特别是由两条未知长度的直线相交时）、尺寸标注、角度标注。

       05.

       审图：需建立两个图层分别是绘图、尺寸标注图层，本题使用RECTANG命令绘制圆角矩形框，计算里框中三个矩形框的各坐标。

       绘图步骤：建立两个图层分别是绘图、尺寸标注图层，使用RECTANG命令和相关坐标绘制圆角矩形框，分别用两点坐标法画三个矩形框，剪切多余的线段；进行尺寸标注。

       重点难点：圆角矩形框画法、剪切多余线段、内框三个矩形每两个坐标的计算。

       第二部分：

       01.

       审图：此图包括外框、里面的一个圆、一个正六边形、一个矩形框、一个多线段框，每个部分都可以计算其坐标和相应尺寸；图层有三个，分别为绘图、尺寸标注、辅助线图层。

       绘图步骤：建立三个图层，分别为绘图、尺寸标注、辅助线图层，使用line的正交模式、极轴追踪模式和相应尺寸完成外框；分别确定圆、正六边形的圆心和中心；确定内矩形框的两点坐标，内多线段框绘图起点坐标（49，-2）完成绘图；最后进行尺寸标注。

       重点难点：圆、正六边形的圆心和中心的定位、各坐标的计算。

       02.

       审图：需要三个图层，分别为绘图、尺寸标注、辅助线图层图层；此图为左右对称图形课通过镜像命令画图，先画左半外框和里面的四个圆即可。

       绘图步骤：建立三个图层，分别为绘图、尺寸标注、辅助线图层，计算各点坐标和各段线段尺寸各圆的圆心坐标，利用line和相关尺寸定位画左半外框，利用c和各圆半径画四个圆，镜像到右边完成画图；最后进行尺寸标注。

       重点难点：各坐标、尺寸长的计算、圆心的确定、两斜线的画法、镜像的使用。

       03.

       审图：需要三个图层，分别为绘图、尺寸标注、辅助线图层图层；此图包括左右两个部分，左边的外框和里面的两个圆都可完成，右边的图形是在左边图形基础上通过偏移相关线条完成。

       绘图步骤：建立三个图层，分别为绘图、尺寸标注、辅助线图层，由点（14,0）开始依次画出各个外框线段，计算两圆的圆心坐标画圆；把左边的图通过复制再通过偏移相关线条和修剪多余线条完成绘图；最后进行尺寸标注。

       重点难点：两段斜线的画法、复制命令的使用、偏移命令的使用。

       第三部分：

       01.

       审图：需要三个图层，分别为绘图、尺寸标注、辅助线图层图层；本图包括四个主要部分两同心圆和上部的圆和直线线框、右边的相切圆弧、由两圆和两段圆弧相切的曲线图形。

       绘图步骤：建立三个图层，分别为绘图、尺寸标注、辅助线图层，通过相应尺寸和旋转角度画出各条辅助线，画左下两同心圆和上部的三个圆利用正交模式和对象捕捉中的切点画出四条竖直直线，修剪多余线段；画出R33的辅助线，定位出各个圆心坐标完成两圆和两段圆弧相切的曲线图形（右里面的图形），修剪多余线段；作R10的圆，再作R6的圆与两圆相切，作一大圆与R10的圆外切，再完成其他圆弧的相切，修剪多余线段；最后进行尺寸标注。

       重点难点：辅助线的定位、各圆心的确定，各圆的相切、多余线段和圆弧的修剪、尺寸标注的布置。

       02.

       审图：需要三个图层，分别为绘图、尺寸标注、辅助线图层图层；本图包括四个组成部分，外框和里面三个图形，相关辅助线、线段、圆尺寸都可确定。

       绘图步骤：建立三个图层，分别为绘图、尺寸标注、辅助线图层，先画出辅助线，再由相关尺寸画出外框，再通过坐标计算确定里面图形的起点坐标（5，22）依次画出各线段，先画两圆再画与之相切的直线再修剪即可；最后进行尺寸标注。

       重点难点：直线与圆的相切、相关坐标的计算、斜线段的画法。

       03.

       审图：需要三个图层，分别为绘图、尺寸标注、辅助线图层图层；这个图的先绘制外框，其余主要采用OFFSET命令和相应尺寸依次画出。

       绘图步骤：建立三个图层，分别为绘图、尺寸标注、辅助线图层；绘制辅助线，利用计算的坐标和原图给的相应线段尺寸完成外框；里面的图形可通过计算相对偏移量来进行相应的偏移即可依次完成各线段的画法，修剪多余线段；最后进行尺寸标注。

       重点难点：各尺寸的计算、各偏移量的确定、辅助线的绘制、多余线段的修剪。

       04.

       审图：需要三个图层，分别为绘图、尺寸标注、辅助线图层图层；本图主要是圆的相切和多余圆弧的修剪，相关圆的圆心、半径的确定。

       绘图步骤：建立三个图层，分别为绘图、尺寸标注、辅助线图层；确定相关尺寸绘制辅助线，先作直径24和R29的圆，再画出图形上部的矩形框和倒角部分；再作R24和R36的圆分别与竖直直线和前面两个圆相切，修剪多余线段和圆弧。用同样的方法画左侧的圆R2和相关的相切圆再修剪多余圆弧即可完成，最后进行尺寸标注。

       重点难点：各圆圆心的确定、使用画圆中的T 画相切圆、相关的尺寸定位、直径和倒角的标注。

       05.

       审图：需要三个图层，分别为绘图、尺寸标注、辅助线图层图层；本图主要是圆的相切和多余圆弧的修剪，相关圆的辅助线、圆心、半径的确定。

       绘图步骤：建立三个图层，分别为绘图、尺寸标注、辅助线图层；确定相关尺寸绘制辅助线，先画两部分直径为14、28

        的两圆，再画直径为17、35的两圆，分别使用通过象限点画水平线与圆相切、使用画圆中的T

       画相切圆完成各部分的直线和圆弧相切；图形的中间部分为两个圆与两段圆弧相切，画法与之前相同。图形最上部圆心的确定是使用辅助线画法来确定，依次可以完成相关圆和圆弧的相切；修剪多余的线段和圆弧即可完成整个图。最后进行尺寸标注。

       重点难点：相关的辅助线尺寸定位、各圆圆心的确定、使用画圆中的T 画相切圆、修剪多余的线段和圆弧、尺寸标注的布置。

       第四部分：总结和心得体会

       时光飞逝，岁月如梭，转眼间我们的CAD课程学习也接近了尾声。这是一门非常实用的课程，知识由浅到深，前面很多的基本操作是比较简单易懂的，后面的综合绘图有点麻烦，但只要按照正确的步骤绘图也是可以完成的。书本上需要记得的东西很多，但是真正在电脑上绘图时可以容易找到相关命令。我想，要学好这门课程也是不容易的，还得多练习，正所谓“绘图之道，唯有于勤；成图之妙，唯有于思”绘图的中心思想就是：用尽可能少的操作完成尽可能多的要求。以下是我在老师的带领下所获得的一些心得和体会。

       经过一个学期的学习，我从画最简单的直线，画圆，到画涂层，再到标注，从最基本的命令line、矩形、圆到后面的偏移、镜像、旋转、拉伸等等，一点一滴地学到了很多关于CAD的知识和技巧，也从一个对于CAD什么都不懂的门外汉变成一个能够独自完成一些比较简单的图形的行内人士了。不过想要学好CAD并非一朝一夕，因为想要能把CAD运用熟练必须靠更多的练习，而不是一时半会就能完成的。因为CAD也是有它的难度所在的，没有长时间的练习是难以成为一个CAD的高手的。

       总的说来，对于CAD，仅仅是知道，了解怎么去使用它是远远不够的，还要时常的练习使用，才能熟能生巧。对于学习CAD，练习时非常重要的。当然，CAD作图的时候，严谨、认真也是很重要的。

       对于画CAD先对复杂的图形，我们只有严谨、认真、仔细地完成每一个步骤，注意每个细节，更多思考以寻求最快速的画法技巧，才能更多节约时间，而且要做到触类旁通。否则很可能在某一步弄错一个数据或者某个位置的定位使得最后整个图都不正确，只好全部重做。所以就算我们已经能够熟练使用CAD了以后还是要认真仔细的对待每一个数据，重视每一步的操作步骤，以免发生这样的错误。绘图不仅要练要思还要总结，为以后提高画图速度打下基础。

如何用python turtle画斐波那契螺旋曲线？

       当turtle.seth(0),箭头指向0，就是→，因为你后面是turtle.fd(-400),面向右方后退400个单位

       turtle.seth(0),箭头指向180，就是←，turtle.fd(400)，-400变为400，就是想要的效果

       我把矩形和圆弧都用不同颜色填充了，你按照自己的需求修改一下吧，你的题目说的不清楚。

#?Python3.6

       #?使用turtle绘制Fibonacci螺旋

       def?draw_fibonacci(x):

       #?F0=1

       #?F1=1

       #?Fn=F（n-1）+F（n-2）

       #?产生斐波那契数列，用于查表

       #?像这种计算复杂性指数增长的计算，不要写个函数去每次求一个数

       #?最好的办法是，按照规律写出查找表，用查找的方法来得到数据

       f_list?=?[]

       for?i?in?range(x):

       if?i?==?0:

       f_list.append(1)

       elif?i?==?1:

       f_list.append(1)

       else:

       f_list.append(f_list[i-1]+f_list[i-2])

       #?像素比例

       f0?=?50

       #?设置画笔属性

       turtle.pensize(5)

       turtle.pencolor("black")

       turtle.penup()

       turtle.home()

       turtle.pendown()

       for?i?in?range(0,?len(f_list)):

       #?绘制速度，1~10个不同速度等级，小于1或者大于10立即绘制

       turtle.speed(1)

       turtle.pendown()

       #?绘制矩形

       if?i?==?0:

       fill_color?=?"black"

       else:

       fill_color?=?(random.random(),?random.random(),?random.random())

       turtle.fillcolor(fill_color)

       turtle.begin_fill()

       turtle.forward(f_list[i]*f0)

       turtle.left(90)

       turtle.forward(f_list[i]*f0)

       turtle.left(90)

       turtle.forward(f_list[i]*f0)

       turtle.left(90)

       turtle.forward(f_list[i]*f0)

       turtle.left(90)

       turtle.end_fill()

       #?绘制圆弧

       fill_color?=?(random.random(),?random.random(),?random.random())

       turtle.fillcolor(fill_color)

       if?i?==?0:

       turtle.forward(f_list[i]?*?f0?/?2)

       turtle.begin_fill()

       turtle.circle(f_list[i]?*?f0?/?2,?360)

       turtle.end_fill()

       #?移动到一下起点

       turtle.forward(f_list[i]?*?f0?/?2)

       continue

       else:

       turtle.begin_fill()

       turtle.circle(f_list[i]?*?f0,?90)

       turtle.left(90)

       turtle.forward(f_list[i]?*?f0)

       turtle.left(90)

       turtle.forward(f_list[i]?*?f0)

       turtle.end_fill()

       #?移动到一下起点

       turtle.speed(0)

       turtle.penup()

       turtle.left(90)

       turtle.forward(f_list[i]?*?f0)

       turtle.left(90)

       turtle.forward(f_list[i]?*?f0)

       turtle.done()

       if?__name__?==?"__main__":

       draw_fibonacci(6)

       下面是我跑出来的结果：

       好了，今天关于“turtle画奥运五环 给了起点坐标”的话题就讲到这里了。希望大家能够对“turtle画奥运五环 给了起点坐标”有更深入的认识，并且从我的回答中得到一些帮助。